|
Evangelos Chatzipantazis Hello visitor! I am Evangelos. My name stems from the Greek Ev (< εύ) + angelos (< ἄγγελος) which translates to "the messenger of good news". So yes; if you are looking for good news you are in the right place. I hold a Master of Science in Robotics from UPenn and a Master of Science in Statistics and Data Science from Wharton. Prior to that, I completed my undergraduate studies in the field of Electrical Engineering and Computer Science at the National Technical University of Athens, under the supervision of Prof. Petros Maragos, where I conducted research on spectral methods for image segmentation. |
|
Research
My current research focuses on learning from geometric data with applications to 3D Computer Vision and Robotics.
More broadly, I am excited about exploiting the structural properties of problems and data to enable efficient learning—both computationally (e.g., via sparsity) and in terms of sample complexity (e.g., through geometric and physical inductive biases).
The methods I developed during my PhD have advanced the field of
Equivariant Deep Learning.
I am also very interested in the use of
Artificial Intelligence for Science. |
|
|
STRiDE: State-space Riemannian Diffusion for Equivariant Planning
Evangelos Chatzipantazis*, Nishanth Rao*, Kostas Daniilidis Learning for Dynamics & Control Conference (L4DC), 2025 PMLR STRiDE is a diffusion-based motion planning framework that operates directly on the state-space manifold, enabling geometry-aware and equivariant planning. The method leverages Riemannian structure to produce plans that are consistent with the underlying symmetries of the system, improving robustness and generalization across transformed task instances. |
|
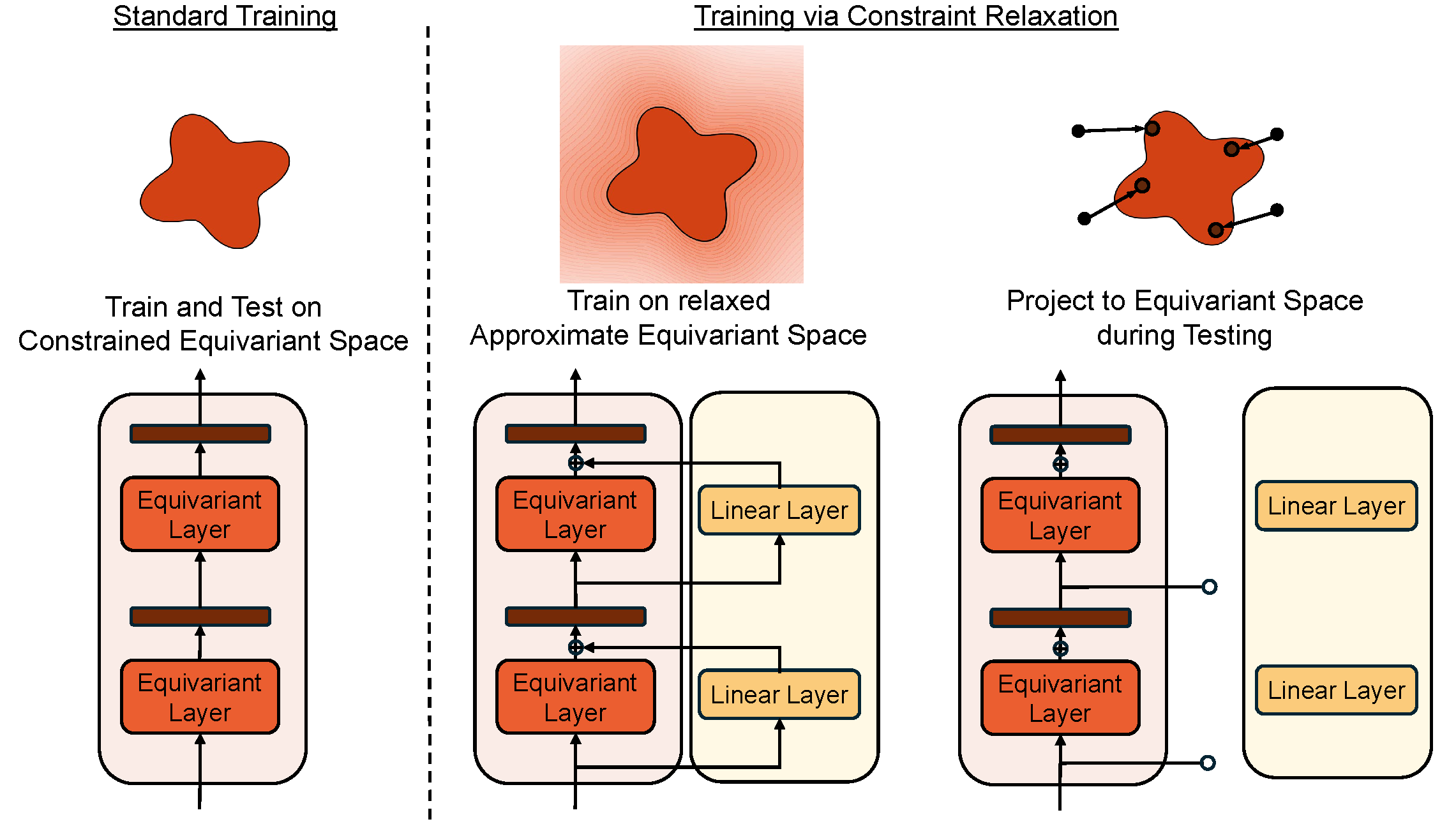
Improving Equivariant Model Training via Constraint Relaxation
Stefanos Pertigkiozoglou*, Evangelos Chatzipantazis*, Shubhendu Trivedi, Kostas Daniilidis Advances in Neural Information Processing Systems (NeurIPS), 2024 Arxiv / OpenReview Introduced a novel method for improving the training of Equivariant Neural Networks. Specifically, we showcased how relaxing the equivariant constraint during training and projecting back to the space of equivariant models during inference can improve the overall optimization |
|
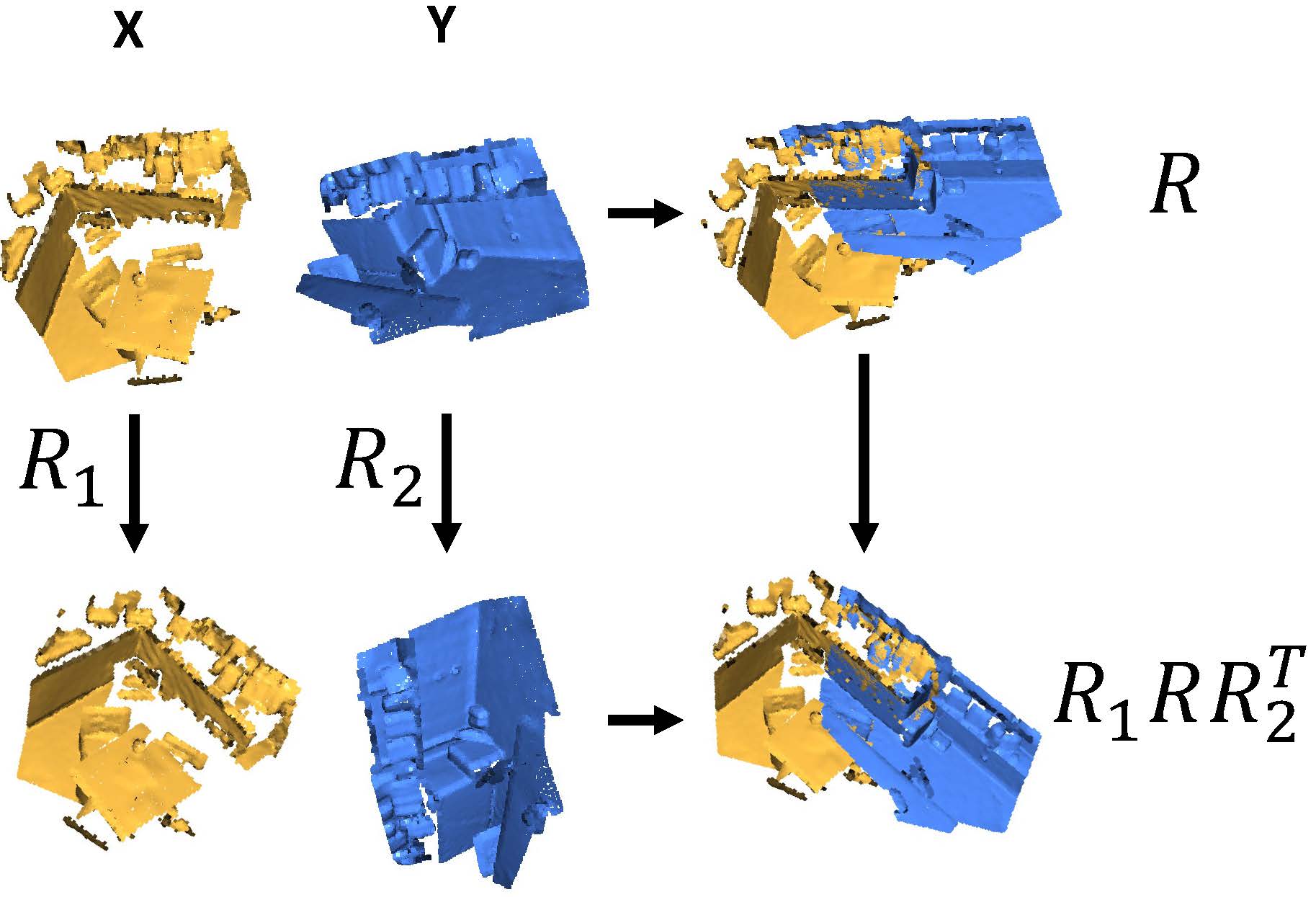
(Oral) BiEquiFormer: Bi-Equivariant Representations for Global Point Cloud Registration
Stefanos Pertigkiozoglou*, Evangelos Chatzipantazis*, Kostas Daniilidis NeurIPS 2024, Workshop on Symmetry and Geometry in Neural Representations (NeuReps) Proccedings Track, 2024 Arxiv Proposed a novel point cloud registration method that utilizes bi-equivariant representations to achieve robust point cloud alignment, that is independent of the initial poses of the input point clouds. |
|
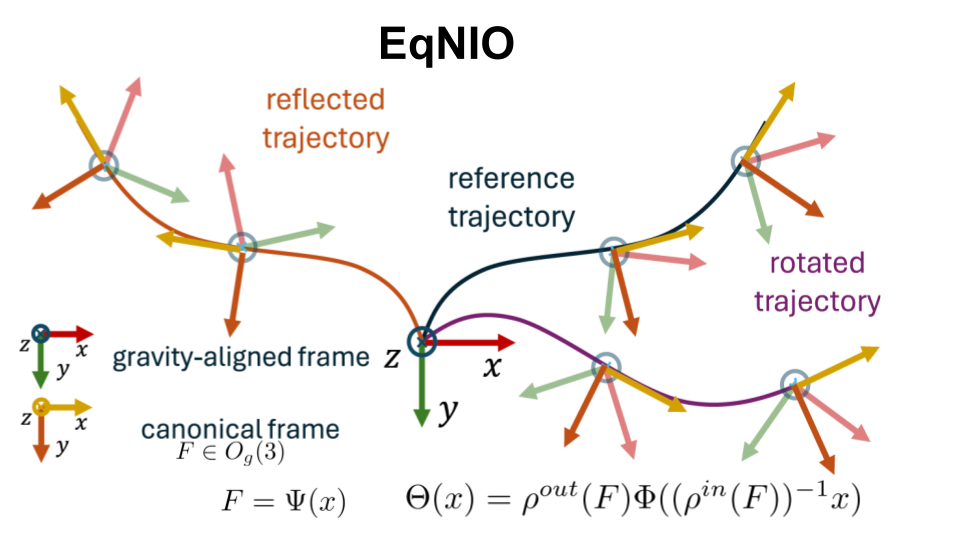
EqNIO: Subequivariant Neural Inertial Odometry
Royina Karegoudra Jayanth*, Yinshuang Xu*, Ziyun Wang, Evangelos Chatzipantazis, Daniel Gehrig, Kostas Daniilidis International Conference on Representation Learning (ICLR) , 2025 arXiv / slides We propose a symmetry-aware inertial odometry framework that exploits IMU roto-reflective equivariances (rotations about gravity and reflections parallel to gravity) via an equivariant gravity-aligned canonicalization, improving TLIO- and RONIN-based performance across multiple datasets. |
|
Structural Risk Minimization for Learning Nonlinear Dynamics
Charis Stamouli, Evangelos Chatzipantazis, George Pappas American Control Conference ACC, 2024 (Best Student Paper Award) arXiv / proceedings / slides We introduce a Structural Risk Minimization framework for nonlinear dynamics that addresses model-class selection by balancing expressivity and learnability, with near-optimal guarantees over a hierarchy of classes and practical instantiations for RKHS and neural networks. |
|
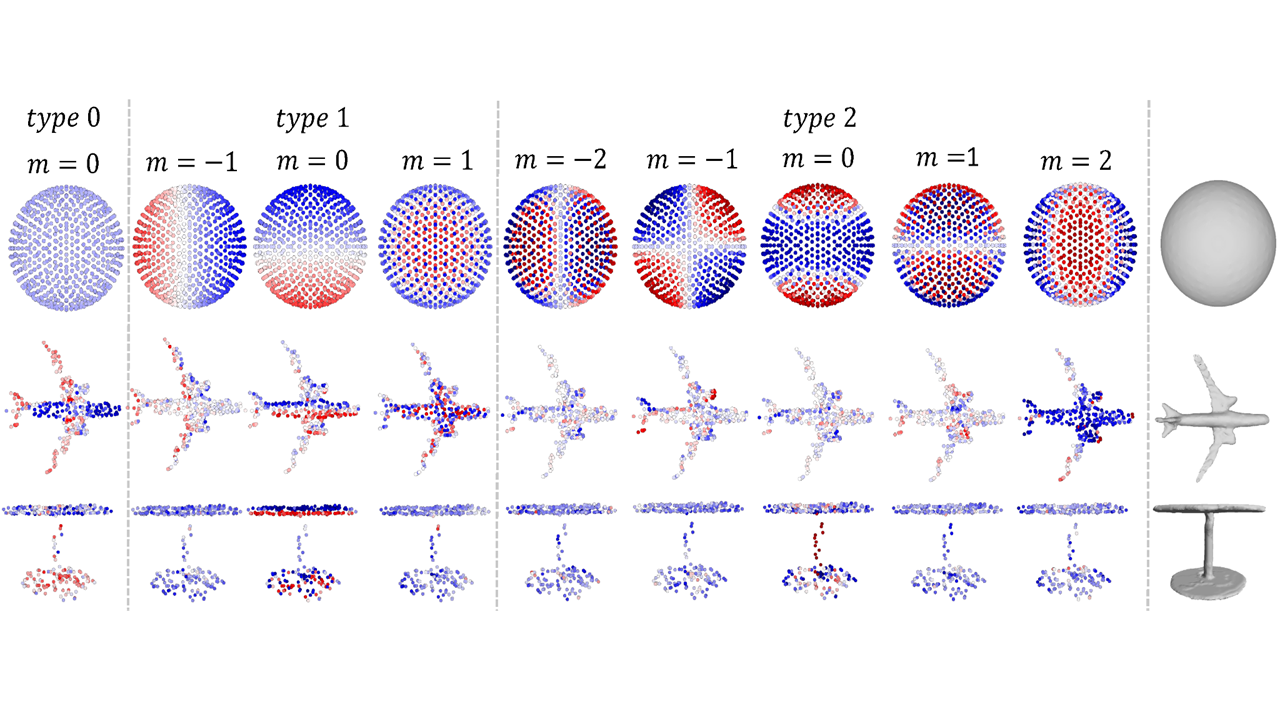
SE(3)-Equivariant Attention Networks for Shape Reconstruction in Function Space
Evangelos Chatzipantazis*, Stefanos Pertigkiozoglou*, Edgar Dobriban, Kostas Daniilidis The Eleventh International Conference on Learning Representations ICLR, 2023 project page / slides / arXiv / openreview Local shape modeling and SE(3)-equivariance are strong inductive biases to reconstruct scenes of arbitrarily many objects appearing in random poses even when a network is trained on single objects in canonical pose. |
|
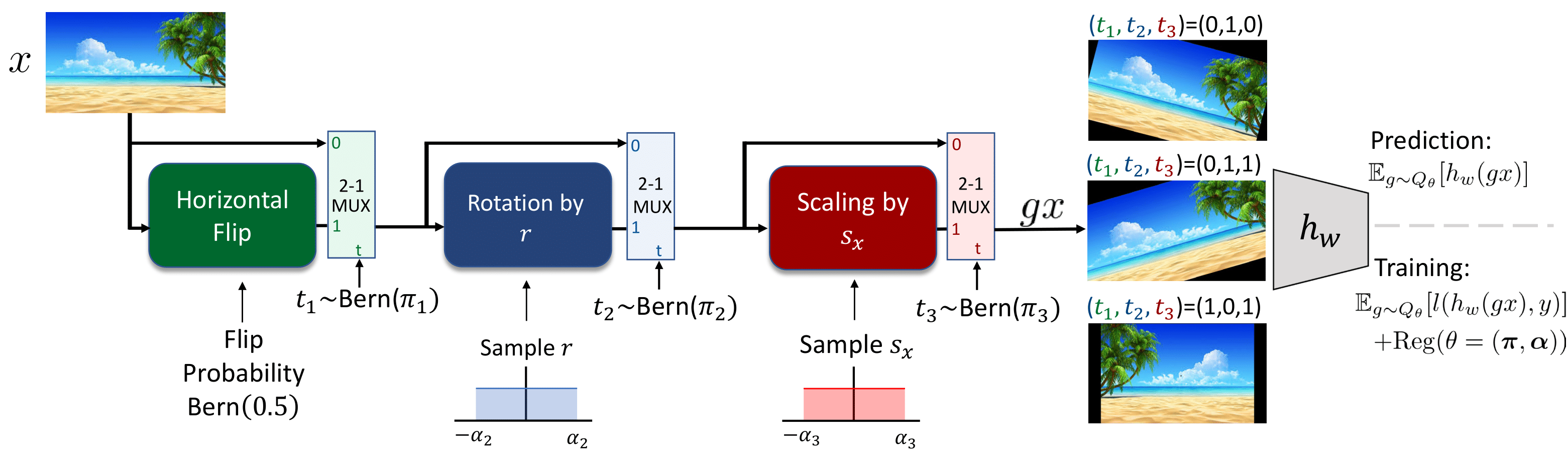
Learning Augmentation Distributions using Transformed Risk Minimization
Evangelos Chatzipantazis*, Stefanos Pertigkiozoglou*, Kostas Daniilidis, Edgar Dobriban, Transactions on Machine Learning Research TMLR, 2023 arXiv / openreview We propose a new Transformed Risk Minimization (TRM) framework as an extension of classical risk minimization. Our TRM method (1) jointly learns transformations and models in a single training loop, (2) works with any training algorithm applicable to standard risk minimization, and (3) handles any transforms, such as discrete and continuous classes of augmentations. To avoid overfitting when implementing empirical transformed risk minimization, we propose a novel regularizer based on PAC-Bayes theory. We propose a new parametrization of the space of augmentations via a stochastic composition of blocks of geometric transforms. The performance compares favorably to prior methods on CIFAR10/100. Additionally, we show empirically that we can correctly learn certain symmetries in the data distribution (recovering rotations on rotated MNIST) and can also improve calibration of the learned model. |
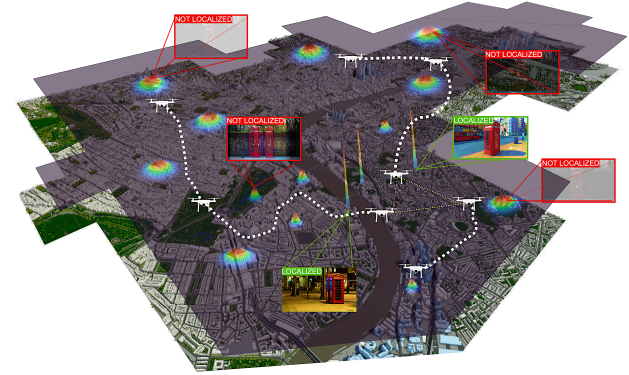
Graph Neural Networks for Multi-Robot Active Information Acquisition
|
Mariliza Tzes, Nikolaos Bousias, Evangelos Chatzipantazis, George J. Pappas IEEE International Conference on Robotics and Automation, ICRA, 2023 (Outstanding Paper Award in Multi-Robot Systems) project page / video / paper / arxiv We propose the Information-aware Graph Block Network (I-GBNet), an Active Information Acquisition adaptation of Graph Neural Networks, that aggregates information over the graph representation and provides sequential-decision making in a distributed manner. Numerical simulations on significantly larger graphs and dimensionality of the hidden state and more complex environments than those seen in training validate the properties of the proposed architecture and its efficacy in the application of localization and tracking of dynamic targets. |
Talks |
